Claude Shannon's original outguessing machine, at the MIT Museum
Legend has it that no one, not the greatest scientific minds of the age, could consistently beat Claude Shannon's outguessing (or "mind-reading") machine at Bell Labs. The machine predicted "random" human choices. But since no one choose randomly, the machine always won its guessing game.
This is, I say, the legend. There are many anecdotes but no published statistics on how well humans fared against the machine. Few who were at Bell Labs in 1953 are around to tell the tale. (A notable exception is David Hagelbarger, who built first outguessing machine. I interviewed him for my book.)
I saw Shannon's machine at the storage facility of the MIT Museum. I wasn't able to play it, of course. That would have been almost impious, for it recorded a final score: Player 3507. Machine 5010.
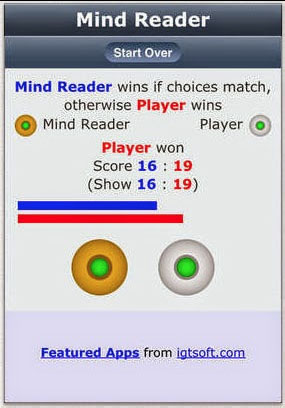
Today, those wanting to experience the outguessing machine have several good virtual options. David Wong has a free app, Mind Reader (ICE factor), available for iOS or Android (left). A browser-based alternative, only a click away, is the "Mind-Reading Program" on the website for Michael Mauboussin's book The Success Equation.
With either you choose one of two alternatives by clicking (Mauboussin's program takes keyboard input as well). If the code predicts your choice, it wins a point; if you fool the computer, you get a point. With Wong's app you play as long as you want. On Mauboussin's site the first to rack up 50 points is the winner. May the best entity win.
The goal is to choose randomly. But almost everyone falls into unconscious patterns. The code keeps track of these and uses them to predict. The basic idea is that past behavior predicts future behavior. Having played both Wong's and Mauboussin's games a while, I can assure you it works. It takes about 25 moves for the machine to learn your play well enough to being predicting effectively. That part of the game is essentially luck (this relates to Mauboussin's book The Success Equation, which asks how to distinguish skill from luck in business and everything else). Thereafter the machine plays relentlessly and almost always reaches 50 points before the human player does—even when it has to overcome a player's early, lucky lead.
I found a way I could beat the machine, much of the time. I'll mention it because it say something about the game's psychology that hasn't, as far as I know, been discussed before.
I reasoned like this: Given that the goal is to play randomly, the game's feedback supplies no useful information. The bars showing who just won and who's ahead are trash talk, a distraction from the goal of being as random as possible. They should be ignored.
I found I did better when I tried to ignore the feedback, and better yet when I made sure I couldn't see the bars. (I resized the window so that the bars weren't visible in Mauboussin's game; covered the top part of my phone screen with Wong's app).
I'm not saying that I succeeded in being random. But, having written a book on the subject, I was at least aware of the common biases. In general we switch back and forth too much between choices and avoid long streaks of the same choice. In a truly random series of 50 binary choices, there is generally a streak of six consecutive identical choices (six "heads" or "tails" in a row). I didn't count, but I made an effort to stick on the same choice repeatedly, relative to what my instincts told me.
By this analysis, the scoring bars are not just a bell or whistle but a crucial part of the outguessing machine. The scoring bars were invented by Shannon's colleague David Hagelbarger, who built the first outguessing machine (above). Hagelbarger was motivated by gameplay considerations. He found that people thought the original machine's game boring until he added two rows of 25 lights across the top. They worked as some pinball machines did: Each time the machine won, a red light came on. Each time the human won, a green light came on. The goal was to light up an entire row of lights before the other.
In this version Hagelbarger's machine (right) became an office hit. Shannon took note and designed his own, improved version. It incorporated a version Hagelbarger's scoring bar. This wasn't lights but a sort of "Newton's cradle" with ball bearings. Shannon's brief publication on the device speaks of "a row of up to fifty balls." I take that to mean that the goal was to get 50 wins before the machine did. The photo's scoring scale runs
. . . . 20. . . . 40. . . . 60. . . . 80. .
That suggests the goal was 100? Maybe this represented percentages, each win counted as 2 percent of the way to victory.
Another part of the outguessing machine legend, which I repeat in Rock Paper Scissors, is that Shannons' machine, which was simpler than Hagelbarger's, was a superior predictor. But the definition of "success" depends greatly on where you place the goal line. It is easier for an outguesser to get to 50 wins first, than to get to 25. My experience with the virtual machines is that they have very little advantage for the first 25 or so moves. I'm now wondering whether the mere fact of setting the goal at 50 wins accounted for Shannon's superior results.
Either way, Hagelbarger latched on to an important concept. We crave positive reinforcement and cringe from negative reinforcement. This is how we learn as infants, children, and adults. Dieters do better with a scale; exercisers appreciate the quantitive data of a Fitbit. The outguessing machines supplied that, though it came with a catch. It encouraged players to frame their choices around "what worked the last time"—or what didn't work. This was indeed central to the Shannon machine's super-concise algorithm.
You might say that Bell Labs' mind-reading machines played a con game on their players. If so, that only made them the more prophetic. Big data is a con game in which it sets the context for the rigged questions it poses. In my book I quote Bell Labs mathematician David Slepian, speaking of Shannon: "My characterization of his smartness is that he would have been the world's best con man."